Elasticity Theory and the Deformation of Two Colliding Disks
Introduction
Elasticity and contact mechanics were first studied in depth during the nineteenth century, later formalized by Russian mathematicians during the back half of the twentieth century. The subject of a deforming solid under stress is quite intriguing, a rather direct application of the topics of complex analysis. Here we study the case of two disks colliding in two dimensions, although many of our results can be generalized to other forms.
I. Solid Mechanics in Two-Dimensions
I.I The Airy Stress Function
For a body in equilibrium, in Einstein’s summation convention:
\begin{equation}\label{force law} \sigma_{ij,j}=0 \end{equation}
The stress tensor for an isotropic, homogenous material is given via Hooke’s law:
\begin{equation}\label{Hooke’s law} \sigma_{ij}=C_{ijkl}\epsilon_{kl}=\lambda\delta_{ij}\epsilon_{kk}+2\mu\epsilon_{ij} \end{equation}
Where \(\epsilon_{ij}\equiv\frac{1}{2}\left(u_{i,j}+u_{j,i}\right)\) is the strain tensor with displacements \(u_i\). Note that both \(\sigma_{ij}\) and \(\epsilon_{ij}\) are symmetric. Now propose functions \(A\) and \(B\) such that:
\begin{equation} B_{,x}=-\sigma_{xy} \nonumber \end{equation}
\begin{equation} B_{,y}=\sigma_{xx} \nonumber \end{equation}
\begin{equation} A_{,x}=\sigma_{yy} \nonumber \end{equation}
\begin{equation} A_{,y}=-\sigma_{yx} \nonumber \end{equation}
Clearly \(A_{,y}=B_{,x}\), so allow \(U_{,x}=A\) and \(U_{,y}=B\). \(U\) is the Airy Stress Function. The following are evident:
\begin{equation} \sigma_{xx}=U_{,yy} \end{equation}
\begin{equation} \sigma_{yy}=U_{,xx} \end{equation}
\begin{equation} \sigma_{xy}=-U_{,xy} \end{equation}
With \eqref{Hooke’s law} we write \(U\) in terms of displacements: \begin{equation} \label{dis uxx} U_{,xx}=\left(\lambda+2\mu\right)\epsilon_{yy}+\lambda\epsilon_{xx}=\left(\lambda+2\mu\right)u_{y,y}+\lambda u_{x,x} \end{equation}
\begin{equation} \label{dis uyy} U_{,yy}=\left(\lambda+2\mu\right)\epsilon_{xx}+\lambda\epsilon_{yy}=\left(\lambda+2\mu\right)u_{x,x}+\lambda u_{y,y} \end{equation}
\begin{equation} \label{dis uxy} U_{,xy}=-2\mu\epsilon_{xy}=-\mu\left(u_{x,y}+u_{y,x}\right) \end{equation}
So with \eqref{dis uxx} and \eqref{dis uyy}: \begin{equation}\label{ux U def} 2\mu u_{x,x} = U_{,yy}- \frac{\lambda}{2\left(\lambda+\mu\right)}U_{,kk} \end{equation}
\begin{equation}\label{uy U def} 2\mu u_{y,y} = U_{,xx}- \frac{\lambda}{2\left(\lambda+\mu\right)}U_{,kk} \end{equation}
Now, from \eqref{Hooke’s law}:
\begin{equation}\label{grad sigma plus} \left(\sigma_{xx}+\sigma_{yy}\right) _{,kk} = \sigma _{xx,xx} + \sigma _{xx,yy} + \sigma _{yy,xx} + \sigma _{yy,yy} = 2\left(\lambda+\mu\right)\left(\epsilon _{xx,xx}+\epsilon _{yy,yy}+\epsilon _{xx,yy}+\epsilon _{yy,xx}\right) \end{equation}
With \eqref{grad sigma plus}:
\begin{equation}\label{sigma sum} \sigma _{xx,yy} + \sigma _{yy,xx} - \frac{\lambda}{2\left(\lambda+\mu\right)} \left(\sigma _{xx}+\sigma _{yy}\right) _{,kk} = 2\mu\left(\epsilon _{xx,yy}+\epsilon _{yy,xx}\right) \end{equation}
With \eqref{Hooke’s law}:
\begin{equation}\label{sigma cross grad} \sigma_{xy,xy} = 2\mu\epsilon_{xy,xy} = 2\mu\left(u_{x,yxy}+u_{y,xxy}\right)=\mu\left(\epsilon_{xx,yy}+\epsilon_{yy,xx}\right) \end{equation}
So, combining \eqref{sigma sum} and \eqref{sigma cross grad}: \begin{equation}\label{full sigma} \sigma _{xx,yy} + \sigma _{yy,xx} - \frac{\lambda}{2\left(\lambda+\mu\right)} \left(\sigma _{xx}+\sigma _{yy}\right) _{,kk} - 2\sigma _{xy,xy} = 0 \end{equation}
With \eqref{force law}: \begin{equation}\label{sigma cross} \sigma_{xx,xx}+\sigma_{xy,yx}+\sigma_{yy,yy}+\sigma_{yx,xy}=0\quad\rightarrow\quad - 2\sigma _{xy,xy} = \sigma _{xx,xx} +\sigma _{yy,yy} \end{equation}
After pairing \eqref{full sigma} and \eqref{sigma cross}:
\begin{equation}\label{grad big sigma} \left( \sigma _{xx} + \sigma _{yy} \right) _{,kk}=0 \end{equation}
\eqref{grad big sigma} has the immediate consequence that \(U\) is biharmonic: \begin{equation} U_{,iijj}=0 \end{equation}
I.II Complex Representations
Define \(P\equiv U_{,kk}\), as \(U\) is biharmonic, \(P_{,kk}=0\); \(P\) is harmonic. Allow \(Q\) to be the harmonic conjugate to \(P\), and from the Cauchy-Reimann Equations:
\begin{equation} P_{,x}=Q_{,y} \nonumber \end{equation}
\begin{equation} P_{,y}=-Q_{,x} \nonumber \end{equation}
Define \(\varphi=p+iq\) such that:
\begin{equation} \varphi_{,z}=\varphi_{,x}=p_{,x}+iq_{,x}=\frac{1}{4}\left(P+iQ\right) \end{equation}
Via Cauchy-Reimann:
\begin{equation} p_{,x}=q_{,y}=\frac{1}{4}P \nonumber \end{equation}
\begin{equation} p_{,y}=-q_{,x}=-\frac{1}{4}Q \nonumber \end{equation}
With \eqref{ux U def} and \eqref{uy U def}:
\begin{equation} 2\mu u_{x,x} = -U_{,xx}+\frac{\lambda+2\mu}{2\left(\lambda+\mu\right)}P \end{equation}
\begin{equation} 2\mu u_{y,y} = -U_{,yy}+\frac{\lambda+2\mu}{2\left(\lambda+\mu\right)}P \end{equation}
Integrating:
\begin{equation} \label{ux U} 2\mu u_{x} = -U_{,x}+\frac{2\left(\lambda+2\mu\right)}{\lambda+\mu}p+C_{1}\left(y\right) \end{equation}
\begin{equation} \label{uy U} 2\mu u_{y} = -U_{,y}+\frac{2\left(\lambda+2\mu\right)}{(\lambda+\mu}q+C_{2}\left(x\right) \end{equation}
From the Cauchy-Reimann Equations:
\begin{equation} 2\mu \left(u_{x,y}+u_{y,x}\right) = -2U_{,xy}+C_{1,y}\left(y\right)+C_{2,x}\left(x\right) \end{equation}
From \eqref{dis uxy}: \begin{equation} C_{1,y}\left(y\right)+C_{2,x}\left(x\right)=0 \end{equation} So, \(C_1\sim y\) and \(C_2\sim x\), corresponding to rigid body displacements which we can safely ignore.
Now consider: \begin{equation} \left(U-xp-yq\right) _{,kk}= U _{,kk} - xp _{,kk} - yq _{,kk} -2p _{,x} - 2q _{,y} \nonumber \end{equation} \begin{equation} = U _{,kk} - xp _{,kk} - yq _{,kk} - P = xp _{,kk} - yq _{,kk} = 0 \nonumber \end{equation} We have used the fact that \(p\) and \(q\) are harmonic as \(p _{,kk} = p _{,xx} +p _{,yy} = q _{,yx} - q _{,xy} = 0\)
So: \begin{equation} U = xp+yq+r \end{equation} Where \(r\) is a harmonic function: \(r_{,kk}=0\).
Now let \(r=\text{Re}\left(\chi\right)\),
\begin{equation}\label{imaginary U} U=\text{Re}\left(\bar{z}\varphi+\chi\right)\quad\rightarrow\quad 2U=\bar{z}\varphi+\chi+z\bar{\varphi}+\bar{\chi} \end{equation}
Using \eqref{imaginary U}:
\begin{equation} \label{Ux im} 2U_{,x}=\varphi+\bar{z}\varphi_{,z}+\chi_{,z}+\bar{\varphi}+z\bar{\varphi}_{,z}+\bar{\chi} _{,z} \end{equation}
\begin{equation} \label{Uy im} 2U_{,y}=i\left(-\varphi+\bar{z}\varphi_{,z}+\chi_{,z}+\bar{\varphi}-z\bar{\varphi}_{,z}-\bar{\chi} _{,z}\right) \end{equation}
Combining \eqref{Ux im} and \eqref{Uy im}: \begin{equation}\label{U complex} U_{,x}+iU_{,y}=\varphi+z\bar{\varphi}_{,z}+\bar{\psi} \end{equation} We have defined, \(\psi\equiv\chi _{,z}\)
Now with \eqref{ux U} and \eqref{uy U}: \begin{equation}\label{ux+uy complex} 2\mu\left(u_{x}+iu_{y}\right)=-\left(U_{,x}+iU_{,y}\right)+\frac{2\left(\lambda+2\mu\right)}{\lambda+\mu}\left(p+iq\right)=\kappa\varphi-z\bar{\varphi}_{,z}-\bar{\psi} \end{equation} Where \(\kappa\equiv\frac{2\left(\lambda+2\mu\right)}{\lambda+\mu}-1=\frac{\lambda+3\mu}{\lambda+\mu}=3-4\sigma\)
We can also express stress components in terms of our complex functions with \eqref{Ux im} and \eqref{Uy im}:
\begin{equation} 2U_{,yy}=2\sigma_{xx}=i\left(-2i\varphi_{,z}+i\bar{z}\varphi_{,zz}+i\psi{,z}-2i\bar{\varphi} _{,z}+iz\bar{\varphi} _{,zz}+iz\bar{\varphi} _{,zz}\right) \end{equation}
\begin{equation} 2U _{,xx}=2\sigma _{yy}=2\varphi _{,z}+\bar{z}\varphi _{,zz}+\psi _{,z}+2\bar{\varphi} _{,z}+z\bar{\varphi} _{,zz}+\bar{\psi} _{,z} \end{equation}
\begin{equation} 2U _{,yx}=-2\sigma _{xy}=i\left(\bar{z}\varphi _{,zz}+\psi _{,z}-z\bar{\varphi} _{,zz}-\bar{\psi} _{,z}\right) \end{equation}
\begin{equation}\label{sigmaxx+sigmayy complex} 2\sigma _{xx} + 2\sigma _{yy} = 4\varphi _{,z}+4\bar{\varphi} _{,z}\quad\rightarrow\quad\sigma _{xx} + \sigma _{yy} = 4\text{Re}\left(\varphi _{,z}\right) \end{equation}
\begin{equation}\label{sigmaxx-sigmayy complex} 2\sigma _{xx} - 2\sigma _{yy}+4i\sigma _{xy}=4\bar{z}\varphi _{,zz}+4\psi{,z}\quad\rightarrow\quad \sigma _{xx} - \sigma _{yy}+2i\sigma _{xy}=2\left(\bar{z}\varphi _{,zz}+\psi _{,z}\right) \end{equation}
Now let’s discuss the arbitrariness of \(\varphi\) and \(\psi\). Suppose we transform \(\varphi\rightarrow\varphi^{'}\) and \(\psi\rightarrow\psi^{'}\).
From \eqref{sigmaxx+sigmayy complex}, \(\varphi^ { '} _{,z}\) must be complex, so \(\varphi^{'} _{,z} = \varphi _{,z} + iD\rightarrow\varphi ^{ ' }=\varphi + iDz + \gamma\) and from \eqref{sigmaxx-sigmayy complex}, \(\psi^{'}=\psi+\gamma^{'}\). Applying \eqref{ux+uy complex}:
\begin{equation} 2\mu\left(u_{x}^{‘}+iu_{y}^{‘}\right)=2\mu\left(u_{x}+iu_{y}\right)\quad\rightarrow\quad \kappa\varphi-z\bar{\varphi}_{,z}-\bar{\psi}=\kappa\varphi^{‘}-z\bar{\varphi}^{‘} _{,z}-\bar{\psi}^{‘} \end{equation} \begin{equation} \rightarrow iDz\left(\kappa +1\right) +\kappa\gamma-\bar{\gamma^{‘}}=0 \end{equation} It is immediately obvious that \(D=0\) and we are free to set either \(\gamma\) or \(\gamma^{'}\), so in principal, this means we can chose \(\varphi\left(0\right)=0\) or \(\psi\left(0\right)=0\), but never both.
II. Solutions for Boundry Problems
II.I Relevant Details From Complex Analysis
We are not going to delve into Complex Analysis too extensively or prove the results here too rigorously as that as has been done ad naseam in a plethora of other sources.
For a complex function \(f\), which is analytic in the simply closed region \(S\) not containing \(\infty\), and continuous outside of \(S\), by Cauchy’s integral theorem: \begin{equation} f(z)=\frac{1}{2\pi i}\oint_\gamma\frac{f\left(t\right)}{t-z}dt\quad z\in S \end{equation} Where \(\gamma\) is the contour around the boundry of \(S\), and \(z\) lies within \(S\), for \(z\) outisde of \(S\), \(\frac{f\left(t\right)}{t-z}\) is analytic, so: \begin{equation}\label{not anal} f(z)=\frac{1}{2\pi i}\oint_\gamma\frac{f\left(t\right)}{t-z}dt=0\quad z\notin S \end{equation}
Now let’s consider a complex function \(g\), which is analytic outside the closed region \(S\), such that \(G\) is analytic at infinity. We can write \(g\) as a Laurent Series for \(z\notin S\):
\begin{equation} g=\sum_{k=0}^\infty a_k z^{-k}\quad z\notin S \end{equation} So for \(z\notin S\): \begin{equation} \oint_\gamma\frac{g\left(t\right)}{t-z}dt =\sum_{k=0}^\infty a_k\oint_\gamma\frac{1}{t^k\left(t-z\right)}dt \end{equation} The integrand, \(\frac{1}{t^k\left(t-z\right)}\) is only singular at \(t=0\) as \(z\notin S\) and \(\gamma\) is a contour around \(S\). By the residue theorem: \begin{equation} =\oint_\gamma\frac{1}{t^k\left(t-z\right)}dt=2\pi i\text{Res}\left(\frac{1}{t^k\left(t-z\right)},t=0\right)=2\pi i \frac{1}{k!}\frac{d^k}{dt^k}\left(\frac{t}{t-z}\right)\left|_{t=0}\right.\quad k>0 \end{equation}
\begin{equation} =-2\pi i \frac{1}{z^k}\quad k>0 \end{equation} We find: \begin{equation} \oint_\gamma\frac{g\left(t\right)}{t-z}dt =-2\pi i\sum_{k=1}^\infty a_kz^{-k} = 2\pi i\left(g\left(\infty\right)-g\left(z\right)\right) \end{equation} In other words: \begin{equation} \label{g inf} g(z)=g\left(\infty\right)-\frac{1}{2\pi i}\oint_\gamma\frac{g\left(t\right)}{t-z}dt \quad z\notin S \end{equation}
Now, lets consider the case where \(S\) is the unit circle, importantly for \(t\) along the boundry of \(S\), \(\bar{t}=\frac{1}{t}\). Now consider \(g^ {'}\left(z\right)\equiv g\left(\frac{1}{z}\right)\), with eqref{g inf}:
\begin{equation} g ^{‘} \left( z \right) = g ^{‘} \left(0\right)-\frac{1}{2\pi i}\oint _\gamma \frac{g ^{‘} \left(\bar{t}\right)}{t-\frac{1}{z}}dt \quad z\notin S \end{equation}
As \(g ^{'}\) is analytic only in \(z\in S\), by \eqref{not anal}, \(g '(z)=0\) in \(z\notin S\), and as \(S\) is the unit circle, \(\frac{1}{z}\) for \(z\notin S\) is equivalent to \(z\) for \(z\in S\). So: \begin{equation} \label{f0 comp} \frac{1}{2\pi i}\oint_\gamma\frac{f\left(\bar{t}\right)}{t-z}dt = f\left(0\right) \quad z\in S \end{equation} Where \(f\) is a function that is analytic for \(z\in S\).
II.II Complex Mapping
In general, we will study a finite region \(S\) in the complex plane, we will move this region to a unit disk in the \(\zeta\) plane, via: \(z=\omega\left(\zeta\right)\). With \eqref{U complex}:
\begin{equation} \varphi\left(\zeta\right)+\frac{\omega\left(\zeta\right)\bar{\varphi}_{,\zeta}\left(\bar{\zeta}\right)}{\bar{\omega} _{,\zeta}\left(\bar{\zeta}\right)}+\bar{\psi}\left(\bar{\zeta}\right)= U _{,x}+iU _{,y} \end{equation}
Now allow \(\varsigma=e^{i\theta}\) to describe the edge of the unit disk in the \(\zeta\) plane. We take the boundary conditions to be given, \(U_{,x}+iU_{,y}=f\) along \(\zeta=\varsigma\), so:
\begin{equation}\label{edge complex varphi psi} \varphi\left(\varsigma\right)+\frac{\omega\left(\varsigma\right)\bar{\varphi} _{,\zeta}\left(\bar{\varsigma}\right)}{\bar{\omega} _{,\varsigma}\left(\bar{\varsigma}\right)}+\bar{\psi}\left(\bar{\varsigma}\right)= f \end{equation}
We will evaluate \(f\) in a later section.
Using a Cauchy’s integral around the unit circle \(\gamma\):
\begin{equation}\label{varphi complex map} \varphi\left(\zeta\right)=\frac{1}{2\pi i}\oint_\gamma\frac{\varphi\left(\varsigma\right)}{\varsigma-\zeta}d\varsigma=-\frac{1}{2\pi i}\oint_\gamma\frac{\omega\left(\varsigma\right)\bar{\varphi}_{,\zeta}\left(\bar{\varsigma}\right)}{\bar{\omega} _{,\zeta}\left(\bar{\varsigma}\right)\left(\varsigma-\zeta\right)}d\varsigma-\frac{1}{2\pi i}\oint _\gamma\frac{\bar{\psi}\left(\bar{\varsigma}\right)}{\varsigma-\zeta}d\varsigma+\frac{1}{2\pi i}\oint _\gamma\frac{f}{\varsigma-\zeta}d\varsigma \end{equation}
With \eqref{f0 comp} and setting \(\bar{\psi}\left(0\right)=0\): \begin{equation} \frac{1}{2\pi i}\oint_\gamma\frac{\bar{\psi}\left(\bar{\varsigma}\right)}{\varsigma-\zeta}d\varsigma=\bar{\psi}\left(0\right)=0 \end{equation}
Defining: \begin{equation} \mathcal{A}\equiv\frac{1}{2\pi i}\oint _\gamma\frac{f}{\varsigma-\zeta}d\varsigma\nonumber \end{equation}
With \eqref{varphi complex map}:
\begin{equation}\label{varphi complex final} \varphi\left(\zeta\right)+\frac{1}{2\pi i}\oint_\gamma\frac{\omega\left(\varsigma\right)\bar{\varphi}_{,\zeta}\left(\bar{\varsigma}\right)}{\bar{\omega} _{,\zeta}\left(\bar{\varsigma}\right)\left(\varsigma-\zeta\right)}d\varsigma=\mathcal{A} \end{equation}
We can take the complex conjugate of \eqref{edge complex varphi psi} to find a similar expression for \(\psi\left(\zeta\right)\), except we cannot remove \(\bar{\varphi}\left(0\right)\) because we have already chosen to set \(\bar{\psi}\left(0\right)=0\).
\begin{equation}\label{psi comp final} \psi\left(\zeta\right)+\bar{\varphi}\left(0\right)+\frac{1}{2\pi i}\oint_\gamma\frac{\bar{\omega}\left(\bar{\varsigma}\right)\varphi_{,\zeta}\left(\varsigma\right)}{\omega _{,\zeta}\left(\varsigma\right)\left(\varsigma-\zeta\right)}d\varsigma=\mathcal{B} \end{equation}
With: \begin{equation} \mathcal{B}\equiv\frac{1}{2\pi i}\oint _\gamma\frac{\bar{f}}{\varsigma-\zeta}d\varsigma\nonumber \end{equation}
II.III Boundry terms
Here we discuss the physical meaning of the \(f=U_{,x}+iU_{,y}\) function. First consider a length of the edge of our body from points \(A\) to \(B\). Considering \(ds\) as an infinitesimal length along the edge of our object, the \(x\) and \(y\) components of the force normal to the length \(AB\) can be found by:
\begin{equation} \label{Fequation} F_i = \int_A^B\sigma_{ij}n_jds \nonumber \end{equation}
Where \(n_i\) is the normal direction pointing out of the solid. The components of the normal vector are found by differentiating since the tangential direction is given by \(t_i\equiv\frac{dx_i}{ds}\), we find:
\begin{equation} n_x=\frac{dy}{ds}\nonumber \end{equation}
\begin{equation} n_y=-\frac{dx}{ds}\nonumber \end{equation}
So: \begin{equation} \sigma_{xj}n_j = \sigma_{xx}\frac{dy}{ds}-\sigma_{xy}\frac{dx}{ds} = U_{,yy}\frac{dy}{ds}+U_{,xy}\frac{dx}{ds} = \frac{d}{ds}\left(U_{,y}\right) \end{equation}
\begin{equation} \sigma_{yj}n_j = \sigma_{yx}\frac{dy}{ds}-\sigma_{yy}\frac{dx}{ds} = -U_{,yx}\frac{dy}{ds}-U_{,xx}\frac{dx}{ds} = -\frac{d}{ds}\left(U_{,x}\right) \end{equation}
And, with \eqref{Fequation}: \begin{equation} F_x+iF_y = \int_A^B\sigma_{xj}n_j+\sigma_{yj}n_jds = \int_A^B\frac{d}{ds}\left(U_{,y}-iU_{,x}\right)ds = -i\left(U_{,x}+iU_{,y}\right) \end{equation}
We can express \(f\) in terms of the force distributions in the \(x\) and \(y\) directions along the surface of our object: \begin{equation} f = U_{,x}+iU_{,y} = i\left(F_x+iF_y\right) \end{equation}
III Solution for a Circular Disk With Point Forces
III.I Complex Mapping
For a circular object centred at \(z=0\) of radius \(R\), clearly \(z=\omega\left(\zeta\right)=R\zeta\). \eqref{varphi complex final} becomes:
\begin{equation}\label{varphi a expand} \varphi\left(\zeta\right)+\frac{1}{2\pi i}\oint_\gamma\frac{\varsigma\bar{\varphi}_{,\zeta}\left(\bar{\varsigma}\right)}{\varsigma-\zeta}d\varsigma=\mathcal{A} \end{equation}
Because \(\varphi\left(\zeta\right)\) is analytic in the unit circle, we express the function as a power series: \(\varphi\left(\zeta\right)=a_0+a_1\zeta+a_2\zeta^2+...\). Using \(\bar{\varsigma}\varsigma=1\) on the unit circle:
\begin{equation} \frac{1}{2\pi i}\oint_\gamma\frac{\varsigma\bar{\varphi}_{,\zeta}\left(\bar{\varsigma}\right)}{\varsigma-\zeta} d\varsigma= \frac{1}{2\pi i}\oint _\gamma\frac{\bar{a_1}\varsigma+2\bar{a_2}}{\varsigma-\zeta}d\varsigma+\sum _{k=3}^\infty\frac{1}{2\pi i}\oint _\gamma\frac{k!\bar{a_k } \bar{\varsigma}^{k-2}}{\varsigma-\zeta}d\varsigma \end{equation}
With \eqref{f0 comp}:
\begin{equation} \frac{1}{2\pi i}\oint _\gamma\frac{\bar{a_k } \bar{\varsigma}^{k-2}}{\varsigma-\zeta}d\varsigma = \bar{a_k} 0^{k-2} = 0 \end{equation}
So, reducing \eqref{varphi a expand} and simplfying integrals:
\begin{equation}\label{varphi simple} \varphi\left(\zeta\right)+\bar{a_1}\zeta+2\bar{a_2}=\mathcal{A} \end{equation}
By definition \(a_1\equiv\varphi_{,\zeta}\left(0\right)\) and \(a_2\equiv\varphi_{,\zeta\zeta}\left(0\right)\), using \eqref{varphi simple}, taking derivatives and setting \(\zeta=0\), we find:
\begin{equation} a_1+\bar{a_1}=\mathcal{A}_{,\zeta}\left(0\right) \nonumber \end{equation}
\begin{equation} \label{a2 comp} a_2=\mathcal{A}_{,\zeta\zeta}\left(0\right) \end{equation}
Only the real part of \(a_1\) is determined, as the imaginary portion cancels in \eqref{varphi simple}. So, we can conveniently set \(\text{Im}\left(a_1\right)=0\) and use:
\begin{equation} \label{a1 comp} a_1=\frac{1}{2}\mathcal{A}_{,\zeta}\left(0\right) \end{equation}
Using \eqref{psi comp final} we can find a similar expression for \(\psi\left(\zeta\right)\), noting that for our circular case:
\begin{equation} \frac{1}{2\pi i}\oint_\gamma\frac{\bar{\varsigma}\varphi_{,\zeta}\left(\varsigma\right)}{\varsigma-\zeta}d\varsigma = \frac{1}{2\pi i}\oint_\gamma\frac{\varphi_{,\zeta}\left(\varsigma\right)}{\varsigma\left(\varsigma-\zeta\right)}d\varsigma \end{equation}
Using a taylor series to expand \(\psi\left(\varsigma\right)\), as it is analytic on the unit disk:
\begin{equation} =\frac{1}{2\pi i}\oint_\gamma\frac{a_1\bar{\varsigma}}{\varsigma-\zeta}d\varsigma+\frac{1}{2\pi i}\oint_\gamma\sum_{k=2}^\infty \frac{ka_k\varsigma^{k-2}}{\varsigma-\zeta}d\varsigma \end{equation}
With \eqref{f0 comp}: \begin{equation} =a_1 0 + \sum_{k=2}^\infty ka_k\zeta^{k-2} = \frac{\varphi_{,\zeta}\left(\zeta\right)}{\zeta}-\frac{a_1}{\zeta} \end{equation}
And:
\begin{equation}\label{psi simple} \psi\left(\zeta\right)+\bar{\varphi}\left(0\right)+\frac{\varphi_{,\zeta}\left(\zeta\right)}{\zeta}-\frac{a_1}{\zeta}=\mathcal{B} \end{equation}
III.II Forcing Terms
We consider a disk under \(n\) concentrated point forces, \(F_i^{\left(1\right)},F_i^{\left(2\right)},...,F_i^{\left(n\right)}\). Each force acts at an edge of the circular disk, \(F_i^{\left(1\right)}\) acts at \(z^{\left(1\right)}=Re^{i\alpha^{\left(1\right)}}\), an so forth, where \(\alpha^{\left(k\right)}\) is an angle along the disk edge. Without loss of generality, let \(\alpha^{\left(1\right)} < \alpha ^{\left(2\right)} < ...< \alpha^{\left(n\right)}\). we can easily move to the unit disk, denoting forces to act at \(\varsigma^{\left(k\right)}=e^{i\alpha^{\left(k\right)}}\).
Along each arc \(\varsigma^{\left(1\right)}\varsigma^{\left(2\right)}\), \(\varsigma^{\left(2\right)}\varsigma^{\left(3\right)}\), …, \(\varsigma^{\left(n\right)}\varsigma^{\left(1\right)}\), \(f\) will be constant, as there are no forces along these arcs. But, \(f=i\left(F_x+iF_y\right)\) will change by \(i\left(F_x^{\left(k\right)}+iF_y^{\left(k\right)}\right)\) when passing through the point \(\varsigma^{\left(k\right)}=e^{i\varsigma^{\left(k\right)}}\). We can set \(f=0\) along \(\varsigma^{\left(n\right)}\varsigma^{\left(1\right)}\), and \(f=i\left(F_x^{\left(1\right)}+iF_y^{\left(1\right)}\right)\) along \(\varsigma^{\left(1\right)}\varsigma^{\left(2\right)}\), \(f=i\left(F_x^{\left(1\right)}+iF_y^{\left(1\right)}\right)+i\left(F_x^{\left(2\right)}+iF_y^{\left(2\right)}\right)\) along \(\varsigma^{\left(2\right)}\varsigma^{\left(3\right)}\) and so fourth. An integral over the unit circle can be split into an integration over each of these arcs:
\begin{equation} \oint _\gamma d\varsigma =\int _{\varsigma^{\left(1\right)}} ^ {\varsigma^{\left(2\right)}} d\varsigma+\int _{\varsigma^{\left(2\right)}} ^ {\varsigma^{\left(3\right)}}d\varsigma+\quad…\quad+\int _{\varsigma^{\left(n\right)}} ^ {\varsigma^{\left(1\right)}}d\varsigma \end{equation}
So, solving for \(\mathcal{A}\): \begin{equation} \mathcal{A} = \frac{1}{2\pi i}\oint _\gamma \frac{f}{\varsigma-\zeta}d\varsigma = \frac{1}{2\pi i}\int _{\varsigma^{\left(1\right)}} ^ {\varsigma^{\left(2\right)}} \frac{f}{\varsigma-\zeta}d\varsigma+\frac{1}{2\pi i}\int _{\varsigma ^{\left(2\right)}} ^{\varsigma ^{\left(3\right)}}\frac{f}{\varsigma-\zeta}d\varsigma+\quad…\quad+\frac{1}{2\pi i}\int _{\varsigma ^ {\left(n\right)}} ^ {\varsigma^{\left(1\right)}} \frac{f}{\varsigma-\zeta}d\varsigma \end{equation}
\begin{equation} = \frac{1}{2\pi}\int _{\varsigma^{\left(1\right)}} ^ {\varsigma^{\left(2\right)}} \frac{F _x^{\left(1\right)}+iF _y^{\left(1\right)}}{\varsigma-\zeta}d\varsigma+\frac{1}{2\pi }\int _{\varsigma^{\left(2\right)}} ^ {\varsigma^{\left(3\right)}} \frac{F _x^{\left(1\right)}+F_x^{\left(2\right)}+iF _y^{\left(1\right)}+iF _y^{\left(2\right)}}{\varsigma-\zeta}d\varsigma\nonumber \end{equation}
\begin{equation} +\frac{1}{2\pi} \int _{\varsigma^{\left(n\right)}} ^ {\varsigma^{\left(1\right)}} \frac{F _x^{\left(1\right)}+…+F _x^{\left(n\right)}+iF _y^{\left(1\right)}+…+iF _y^{\left(n\right)}}{\varsigma-\zeta}d\varsigma \end{equation}
\begin{equation} = \frac{F_x^{\left(1\right)}+iF _y^{\left(1\right)}}{2\pi}\ln{\frac{\varsigma ^ {\left(2\right)}-\zeta}{\varsigma ^ {\left(1\right)}-\zeta}} + \frac{F_x^{\left(1\right)}+F_x^{\left(2\right)}+iF_y^{\left(1\right)}+iF_y^{\left(2\right)}}{2\pi}\ln{\frac{\varsigma ^ {\left(3\right)}-\zeta}{\varsigma ^ {\left(2\right)}-\zeta}}+\quad … \nonumber \end{equation}
\begin{equation} +\frac{F_x^{\left(1\right)}+…+F_x^{\left(n\right)}+iF_y^{\left(1\right)}+…+iF_y^{\left(n\right)}}{2\pi}\ln{\frac{\varsigma ^ {\left(1\right)}-\zeta}{\varsigma ^ {\left(n\right)}-\zeta}} \end{equation}
We rewrite to find:
\begin{equation}\label{A equation} \mathcal{A}=-\frac{1}{2\pi}\sum_{k=1}^{n} \left(F_x^{\left(k\right)}+iF _y^{\left(k\right)}\right)\ln{\left(\varsigma ^ {\left(k\right)}-\zeta\right)} \end{equation}
And similarly:
\begin{equation}\label{B equation} \mathcal{B}=\frac{1}{2\pi}\sum_{k=1}^{n} \left(F_x^{\left(k\right)}-iF _y^{\left(k\right)}\right)\ln{\left(\varsigma ^ {\left(k\right)}-\zeta\right)} \end{equation}
Solving for \(a_1\) and \(a_2\) using \eqref{a2 comp} and \eqref{a1 comp}:
\begin{equation} a_1=\frac{1}{4\pi}\sum_{k=1}^{n} \frac{F_x^{\left(k\right)}+iF _y^{\left(k\right)}}{\varsigma ^ {\left(k\right)}}=\bar{a_1}=\frac{1}{4\pi}\sum _{k=1}^{n} \left(F_x^{\left(k\right)}-iF _y^{\left(k\right)}\right)\varsigma ^ {\left(k\right)} \end{equation}
\begin{equation} a_2=\frac{1}{2\pi}\sum_{k=1}^{n} \frac{F_x^{\left(k\right)}+iF _y^{\left(k\right)}}{\left(\varsigma ^ {\left(k\right)}\right)^2} \end{equation}
With \eqref{varphi simple} and \eqref{psi simple}:
\begin{equation}\label{varphi final eq} \varphi\left(\zeta\right)=\mathcal{A}-a_1\zeta-2\bar{a_2} \end{equation} \begin{equation}\label{psi final eq} \psi\left(\zeta\right)=\mathcal{B}+\frac{2a_1}{\zeta}-\frac{\mathcal{A}_{,\zeta}}{\zeta}-\bar{\mathcal{A}}\left(0\right)+2\bar{a_2} \end{equation}
We have used \(a_1=\bar{a_1}\).
III Specific Solution in the Case of Two Opposing Point Forces
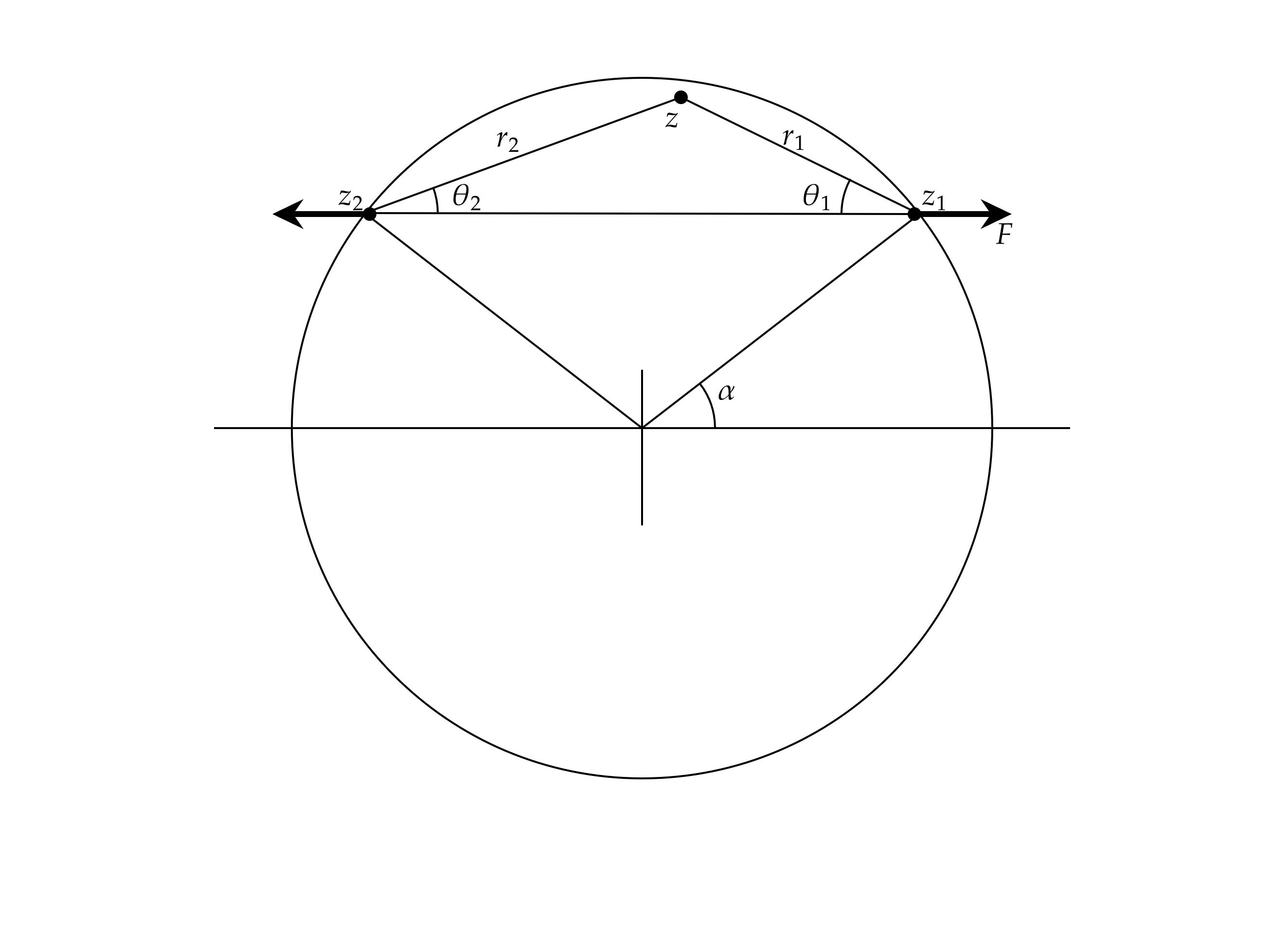
We could in principle approach a circle acted on by \(n\) point forces, but for simplicity, let’s take there to be two opposing forces, parallel to the \(x\) axis acting on the disk at points \(z_1=Re^{i\alpha}\) and \(z_2=Re^{i\left(\pi-\alpha\right)}\). So, \(F_x^{\left(1\right)}=F\) at \(z_1=Re^{i\alpha}\) and \(F_x^{\left(2\right)}=-F\) at \(z_2=Re^{i\left(\pi-\alpha\right)}\). There are no force components in the \(y\) direction.
With \eqref{A equation} and \eqref{B equation}: \begin{equation} \mathcal{A}=-\frac{F}{2\pi}\left(\ln{\left(\varsigma ^ {\left(1\right)}-\zeta\right)}-\ln{\left(\varsigma ^ {\left(2\right)}-\zeta\right)}\right) \end{equation} \begin{equation} \mathcal{B}=-\mathcal{A} \end{equation}
Using \eqref{varphi final eq} and \eqref{psi final eq}: \begin{equation} \varphi\left(\zeta\right)=-\frac{F}{2\pi}\left(\ln{\left(\varsigma ^ {\left(1\right)}-\zeta\right)}-\ln{\left(\varsigma ^ {\left(2\right)}-\zeta\right)}+\frac{\varsigma ^ {\left(1\right)}-\varsigma ^ {\left(2\right)}}{2}\zeta\right) \end{equation} \begin{equation} \psi\left(\zeta\right)=\frac{F}{2\pi}\left(\ln{\left(\varsigma ^ {\left(1\right)}-\zeta\right)}-\ln{\left(\varsigma ^ {\left(2\right)}-\zeta\right)}-\frac{\zeta}{\varsigma ^ {\left(1\right)}-\zeta}+\frac{\zeta}{\varsigma ^ {\left(2\right)}-\zeta}\right)+\frac{\varsigma ^ {\left(1\right)}-\varsigma ^ {\left(2\right)}}{\zeta} \end{equation}
Note that we have removed constant terms, as these result in translational displacement.
And finding the displacements with \eqref{ux+uy complex} after a bit of simplification becomes: \begin{equation} 2\mu\left(u_{x}+iu_{y}\right)=\kappa\varphi-z\bar{\varphi}_{,z}-\bar{\psi} \end{equation}
\begin{equation}\label{u+v long comp} =\frac{F}{2\pi}\left(\ln{\left(\kappa\frac{\varsigma ^ {\left(2\right)}-\zeta}{\varsigma ^ {\left(1\right)}-\zeta}\right)}+\ln{\left(\kappa\frac{\bar{\varsigma} ^ {\left(2\right)}-\bar{\zeta}}{\bar{\varsigma} ^ {\left(1\right)}-\bar{\zeta}}\right)}+\frac{\varsigma ^ {\left(1\right)}-\zeta}{\bar{\varsigma} ^ {\left(1\right)}-\bar{\zeta}}-\frac{\varsigma ^ {\left(2\right)}-\zeta}{\bar{\varsigma} ^ {\left(2\right)}-\bar{\zeta}}-\left(\kappa-1\right)\zeta\text{Re}\left(\varsigma ^ {\left(1\right)}\right)\right) \end{equation}
We can separate the real and imaginary components of \eqref{u+v long comp}, and replacing \(\kappa=\frac{\lambda+3\mu}{\lambda+\mu}\)
\begin{equation}\label{u_x long} u_{x}=\frac{F}{4\pi\mu}\left(\frac{2\left(\lambda+2\mu\right)}{\lambda+\mu}\ln\left(\frac{r_2}{r_1}\right)+\cos{2\theta_1}-\cos{2\theta_2}-\frac{2\mu\cos{\alpha}}{\lambda+\mu}\frac{x}{R}\right) \end{equation} \begin{equation} u_{y}=\frac{F}{4\pi\mu}\left(\frac{2\mu}{\lambda+\mu}\left(\theta_1+\theta_2\right)-\sin{2\theta_1}-\sin{2\theta_2}-\frac{2\mu\cos{\alpha}}{\lambda+\mu}\frac{y}{R}\right) \end{equation}
We have introduced several variables outlined in the diagram below:
IV. The Problem of Two Colliding Disks
Let us consider a point on the circumference of our circular disk. In polar coordinates, let this point have radius \(R\) and angle \(\phi\). With trigonometric relations:
\begin{equation} r_1^2=2R^2\left(1-\cos{\left(\phi-\alpha\right)}\right) \end{equation}
\begin{equation} r_2^2=2R^2\left(1-\cos{\left(\pi-\left(\phi+\alpha\right)\right)}\right) \end{equation}
\begin{equation} \frac{r_2}{r_1}=\pm\sqrt{\frac{1+\cos{\left(\phi+\alpha\right)}}{1-\cos{\left(\phi-\alpha\right)}}}=\pm\frac{\cos{\left(\frac{1}{2}\left(\phi+\alpha\right)\right)}}{\sin{\left(\frac{1}{2}\left(\phi-\alpha\right)\right)}} \end{equation}
The \(+\) in the \(\pm\) accounts for \(\phi>\alpha\) and the \(-\) the inverse. Furthermore:
\begin{equation} \cos{2\theta_1}-\cos{2\theta_2}=-2\cos{\alpha}\cos{\phi} \end{equation}
We can rewrite \eqref{u_x long}:
\begin{equation} u_{x}=-F\frac{\lambda+2\mu}{2\pi\mu\left(\lambda+\mu\right)}\left(\ln\left(\tan{\left(\frac{|\phi-\alpha|}{2}\right)}\right)+\ln\left(\tan{\left(\frac{|\phi+\alpha|}{2}\right)}\right)+2\cos{\alpha}\cos{\phi}\right) \end{equation}
Now, let’s suppose instead of a concentrated force \(F\), there is a force distribution, \(p\left(\phi\right)\). Let us first write this distribution as acting from \(0\) to \(\phi_0\), integrating with polar coordinates:
\begin{equation} u_{x}=-RK\int_0^{\phi_0}\left(\ln\left(\tan{\left(\frac{|\alpha-\phi|}{2}\right)}\right)+\ln\left(\tan{\left(\frac{|\alpha+\phi|}{2}\right)}\right)+2\cos{\alpha}\cos{\phi}\right)p\left(\phi\right)d\phi \end{equation}
Where \(K=\frac{\lambda+2\mu}{2\pi\mu\left(\lambda+\mu\right)}\). Using symmetry, \(p\left(\phi\right)=p\left(-\phi\right)\)
\begin{equation} u_{x}=-RK\int_{-\phi_0}^{\phi_0}\left(\ln\left(\tan{\left(\frac{|\alpha-\phi|}{2}\right)}\right)\cos{\alpha}+\cos{\phi}\right)p\left(\phi\right)d\phi \end{equation}
Now, let’s consider the case of two colliding disks. Marking displacements with \(_1\) and \(_2\) subscripts, and taking \(p\) to be in the negative direction, indenting the circle:
\begin{equation}\label{u_1 eq} u_{x\quad 1}=R_1K_1\int_{-\phi_0}^{\phi_0}\left(\ln\left(\tan{\left(\frac{|\alpha_1-\phi_1|}{2}\right)}\right)+\cos{\alpha_1}\cos{\phi_1}\right)p_1\left(\phi_1\right)d\phi_1 \end{equation}
\begin{equation}\label{u_2 eq} u_{x\quad 2}=R_2K_2\int_{-\phi_0}^{\phi_0}\left(\ln\left(\tan{\left(\frac{|\alpha_2-\phi_2|}{2}\right)}\right)+\cos{\alpha_2}\cos{\phi_2}\right)p_2\left(\phi_2\right)d\phi_2 \end{equation}
Now let \(s\) or \(t\) be a point along the circumference of both disks in the region of contact: \begin{equation} s=R_1\phi_1=R_2\phi_2\nonumber \end{equation} \begin{equation} t=R_1\alpha_1=R_2\alpha_2\nonumber \end{equation} Hence: \begin{equation} p_1\left(\phi_1\right)=p_1\left(\frac{s}{R_1}\right)=p_2\left(\frac{s}{R_2}\right)=p\left(s\right) \end{equation}
Now according to the contact criteria, at all points along the compressed area \begin{equation}\label{disp rule} u_1\left(t\right)+u_2\left(t\right)+d=\left(R_1-x_1\left(t\right)\right)+\left(R_2-x_2\left(t\right)\right) \end{equation} Where \(d\) is the normal approach or displacement between the two disks.
Combining \eqref{u_1 eq} and \eqref{u_2 eq} together with \eqref{disp rule}:
\begin{equation} K_1\int_{-s_0}^{s_0}\left(\ln\left(\tan{\left(\frac{|t-s|}{2R_1}\right)}\right)+\cos{\frac{t}{R_1}}\cos{\frac{s}{R_1}}\right)p\left(s\right)ds\nonumber \end{equation}
\begin{equation} +2K_2\int_{-s_0}^{s_0}\left(\ln\left(\tan{\left(\frac{|t-s|}{2R_2}\right)}\right)+\cos{\frac{t}{R_2}}\cos{\frac{s}{R_2}}\right)p\left(s\right)ds+d\nonumber \end{equation}
\begin{equation}\label{complex integral t and s} =R_1\left(1-\cos{\frac{t}{R_1}}\right)+R_2\left(1-\cos{\frac{t}{R_2}}\right) \end{equation}
\eqref{complex integral t and s} is difficult to solve analytically, but if the contact arc is small, \(s_0\lll R_1, R_2\), we can expand to first order:
\begin{equation} -\left(K_1+K_2\right)\int_{-s_0}^{s_0}\ln\left(\frac{1}{|t-s|}\right)p\left(s\right)ds-P\left(K_1\ln{2R_1}+K_2\ln{2R_2}\right)+P\left(K_1+K_2\right)-P\left(\frac{K_1}{2R_1^2}+\frac{K_2}{2R_2^2}\right)t^2\nonumber \end{equation}
\begin{equation} +d=\frac{1}{2}\left(\frac{1}{R_1}+\frac{1}{R^2}\right)t^2 \end{equation}
Where \(P=\int_{-s_0}^{s_0}p\left(s\right)ds\) is the total applied force magnitude. We can write:
\begin{equation} A\equiv P\left(1-\frac{K_1}{K_1+K_2}\ln{2R_1}-\frac{K_2}{K_1+K_2}\ln{2R_2}\right)+\frac{d}{K_1+K_2} \nonumber \end{equation}
\begin{equation} B\equiv \frac{1}{2\left(K_1+K_2\right)}\left(\left(\frac{1}{R_1}+\frac{1}{R_2}\right)+P\left(\frac{K_1}{R_1^2}+\frac{K_2}{R_2^2}\right)\right) \nonumber \end{equation}
\begin{equation}\label{simplified indent} \int_{-s_0}^{s_0}\ln\left(\frac{1}{|t-s|}\right)p\left(s\right)ds=A-Bt^2 \end{equation}
\eqref{simplified indent} is solved by the following: \begin{equation} p\left(t\right)=\frac{2P}{\pi s_0^2}\sqrt{s_0^2-t^2} \end{equation}
\begin{equation} s_0=\sqrt{\frac{P}{B}} \end{equation}
As \(B\) is constant, given a force \(P\) pushing our disks together, the contact half-width, \(s_0\) and pressure distribution \(P\left(t\right)\) can be found. The indentation depth can also be measured:
\begin{equation} d=P\left(K_1\ln{2R_1}+K_2\ln{2R_2}+\left(K_1+K_2\right)\ln{\left(\sqrt{\frac{4d}{P}}\right)}-\frac{1}{2}\left(K_1+K_2\right)\right) \end{equation}
Note that in the limit of large \(R_1\) and \(R_2\), the above formulas reduce to Hertzian solutions for contacting cylinders. Removing \(R_i^{-2}\) terms: \begin{equation} B\simeq \frac{1}{2\left(K_1+K_2\right)}\left(\frac{1}{R_1}+\frac{1}{R_2}\right) \end{equation} \begin{equation} \rightarrow s_0\simeq\sqrt{2P\left(K_1+K_2\right)\left(\frac{1}{R_1}+\frac{1}{R_2}\right)^{-1}}=\sqrt{\frac{4RF}{\pi E^{*}}} \end{equation}
Where \(R=\left(\frac{1}{R_1}+\frac{1}{R_2}\right)^{-1}\) and \(E^{*}=\left(\frac{1-\nu_{1}^{2}}{E_{1}}+\frac{1-\nu_{2}^{2}}{E_{2}}\right)^{-1}\), the Hertzian solution. Similarly: \begin{equation} d\simeq2\left(K_1+K_2\right)F=\frac{4F}{\pi E^{*}} \end{equation}
Sources
I mainly followed Muskhelishvili’s Some Basic Problems of the Mathematical Theory of Elasticity 1977.