Simulating Jellyfish Feeding Efficiency

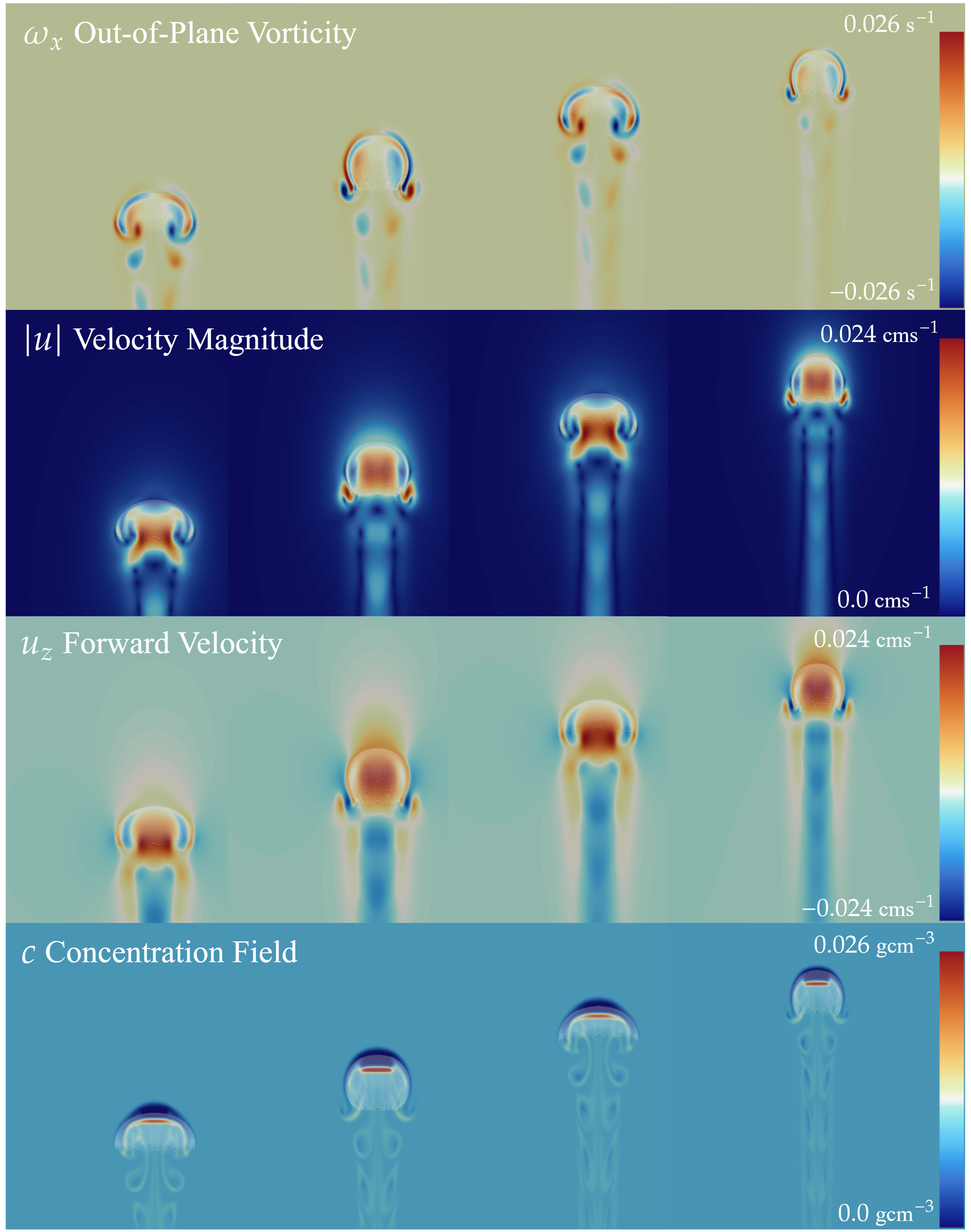
Currently, I am working with the Dunkel group through MIT’s Summer Program for Undergraduate Research (SPUR), where I am investigating nutrient transport in feeding jellyfish via fluid dynamic simulations. During locomotion, jellyfish generate vortex rings that both propel the jellyfish forward and pull nutrient-rich fluid toward the jellyfish’s underside for consumption. This project examines the coupling between paddling kinematics and nutrient uptake. An energy cost can be calculated for distinct paddling gaits, which the jellyfish must then recover with energy obtained from the ingested food. By varying over paddling motion and frequencies, the project aims to optimise food transport dynamics, showing that simulated results match observational jellyfish studies.

The underlying modelling challenge is a fluid-solid interaction problem in which the jellyfish body dynamically interacts with the surrounding fluid. In fluid-solid simulations, both the fluid and solid domains need to be evolved while enforcing interfacial momentum exchange. The current research approach to model jellyfish is the immersed boundary technique, in which the solid phase is represented a Lagrangian force density embedded within an Eulerian fluid domain. Simulations are performed using IBAMR , a high-performance, parallelised implementation of the immersed boundary method that uses adaptive mesh refinement to resolve small-scale features near the fluid-solid interface.

So far, I’ve compared paddling motions and feeding dynamics for two jellyfish species, Aurelia Aurita (moon jellyfish), and the smaller Clytia Hemisphaerica. Specific bell deformations were extracted from recordings via point-tracking and encoded as prescribed deformations in our model. We have found that the larger, A. Aurita, feeds optimally at lower paddling frequencies (~1 Hz). In contrast, the smaller C. Hemisphaerica feeds more effectively at higher paddling frequencies (~10 Hz), consistent with the different size scales and Reynold’s number regime for the two species.

My project report can be found here and my presentation is available here.